Indice
Algorithm Engineering A.A. 2020-2021
 Teacher: Paolo Ferragina
Teacher: Paolo Ferragina
CFU: 9 (first semester).
Course ID: 531AA.
Language: English.
Degree: Master degree in Computer Science and Master degree in CS&Networking.
Question time: Monday: 15-17, or by appointment (given COVID-19 situation, it will occur in video-conferencing within the virtual room of the course)
News: about this course will be distributed via a Telegram channel.
Official lectures schedule: The schedule and content of the lectures is available below and with the official registro.
Goals
In this course we will study, design and analyze advanced algorithms and data structures for the efficient solution of combinatorial problems involving all basic data types, such as integers, strings, (geometric) points, trees and graphs. The design and analysis will involve several models of computation— such as RAM, 2-level memory, cache-oblivious, streaming— in order to take into account the architectural features and the memory hierarchy of modern PCs and the availability of Big Data upon which those algorithms could work on. We will add to such theoretical analysis several other engineering considerations spurring from the implementation of the proposed algorithms and from experiments published in the literature.
Every lecture will follow a problem-driven approach that starts from a real software-design problem, abstracts it in a combinatorial way (suitable for an algorithmic investigation), and then introduces algorithms aimed at minimizing the use of some computational resources like time, space, communication, I/O, energy, etc. Some of these solutions will be discussed also at an experimental level, in order to introduce proper engineering and tuning tools for algorithmic development.
Week Schedule of the Lectures
| Week Schedule | ||
|---|---|---|
| Day | Time Slot | Room |
| Monday | 9:00 - 11:00 | Virtual Room of the course |
| Tuesday | 11:00 - 13:00 | Virtual Room of the course (as above) |
| Wednesday | 11:00 - 13:00 | Virtual Room of the course (as above) |
Exam
News: We will have one midterm exam in November and one in December, this will be done virtually via MS forms with a set of questions and a short time to answer. At the end of the midterm, you'll have also to upload the papers in which you sketched the calculations/simulations that allowed you to get your solutions/answers. The two midterms will be combined with an oral exam to be given in December/January.
The exam will consist of a written pre-test (up to 1hr) and an oral discussion on the pre-test and the whole course program.
| Dates | Room | Text | Notes |
|---|---|---|---|
| 11.11.2020, start at 11:00 | virtual | MidTerm exam: text, results, solution | Students with vote >=16 can participate to the final midterm, the two votes will be averaged. |
| 16.12.2020, start at 11:00 | virtual | FinalTerm exam: text, results, solution | In January, the students who got an average >= 18 will need to pass an oral exam, which can increase or decrease the final vote (by few points). The optional coding contest described above can allow students to increase their final vote. Students can attend the oral in any next exam date of the Winter exam session. |
| 20.01.2021, start at 11:00 | virtual | text, results, solution. | The agenda to book participation to the oral exam is here (deadline to book is 22.01 friday). All communications will occur also via Telegram channel of the course (see above). |
| 10.02.2021, start at 11:00 | virtual (details on esami.unipi.it) | text, results, solution | Students that have to perform the written exam have to connect to the virtual room of the course at the date and hour specified here on the side. Students that have to perform the oral exam in February have to still “register” at the written exam-date on the ESAMI portal by writing in the field “notes”: “only oral”. Then they have to book their oral also on the agenda. All communications will occur also via Telegram channel of the course (see above). |
| 08.06.2021, start at 9:00 | virtual (details on esami.unipi.it) | text, results, solution | The written exam will occur at room O, in Polo Fibonacci. Students that cannot physically attend, are allowed to take the written exam via Teams in the virtual room of the course (as occurred in the previous months) during the same time slot as the physical exam. Oral exams may also occur virtually or physically (in room O too). Please specify in the “notes” when you subscribe to the exam whether you'll attend physically or virtually, distinguishing both the cases of oral and of written exam. Students that have to perform just the oral exam have ALSO to “register” at the written exam-date on the ESAMI portal by writing in the field “notes”: “only oral” and specify whether they'll attend it physically or virtually. Then they have to book their oral also on the agenda. All communications will occur also via Telegram channel of the course (see above). |
| 08.07.2021, start at 9:00 | virtual (details on esami.unipi.it) | text, results, solution | See above |
Coding Project (discretionary)
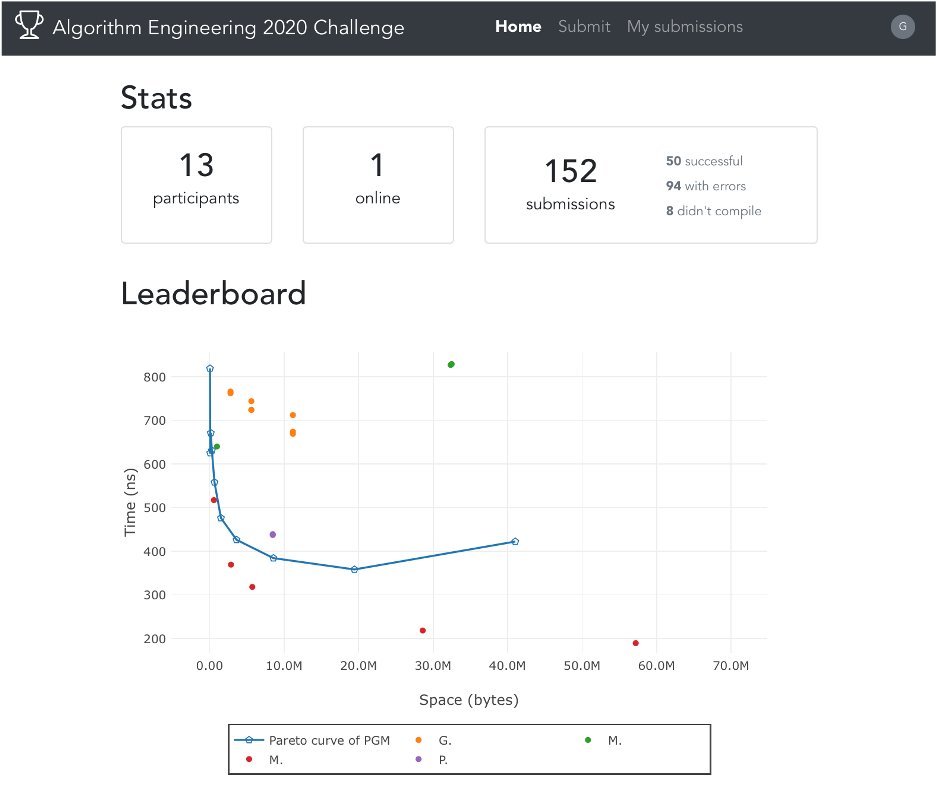
This year students can participate to an (discretionary) coding project in which they have to design-engineer-implement a compressed and learned index for the predecessor search problem (see survey) by deploying advanced libraries (such as SDSL-lite), an available learned index (i.e. the PGM-index) and, of course, the knowledge acquired during the course.
This will be organized in the form of a coding contest (C, C++) so that you will be also provided with a baseline (the PGM-index, indeed) against which to compete, a machine on which running your experiments, and a collection of datasets in order to test your proposals.
Students can participate alone or in groups of two.
The students/groups that will improve the space-time Pareto curve of the PGM-index will be awarded by some points to be added to the final exam ranking: +3 for the top-5 results (where “top” is a combination between time/space performance and algorithmic elegance), +2 for the ones up to the top-15 results, +1 the others (including the ones that just propose an interesting algorithmic solution to the predecessor problem via compressed and learned indexes).
Discussing the project, the design, and the implementation with other students is allowed and encouraged, but your code must be your own. The instructors will evaluate each final submission for originality and correctness.
Details will be provided on a set of web pages prepared by the teaching assistant Giorgio Vinciguerra (email: giorgio.vinciguerra@phd.unipi.it):
* https://github.com/gvinciguerra/AE2020-tutorial - A repository containing code and instructions to set up an environment to experiment with the Succinct Data Structure Library (sdsl).
* Slides of the lab lectures with an explanation of the Challenge (part 1, part 2).
* Video-recordings are also available in the repository of the course.
* A screenshot of the web page of the contest follows below, just to give an idea of the platform we set up to make students compete and evaluate the performance of their codes:
Background and Notes of the Course
I strongly suggest refreshing your knowledge about basic Algorithms and Data Structures by looking at the well-known book Introduction to Algorithms, Cormen-Leiserson-Rivest-Stein (third edition). Specifically, I suggest you look at the chapters 2, 3, 4, 6, 7, 8, 10, 11 (no perfect hash), 12 (no randomly built), 15 (no optimal BST), 18, 22 (no strongly connected components). Also, you could look at the Video Lectures by Erik Demaine and Charles Leiserson, specifically Lectures 1-7, 9-10, and 15-17.
We'll use the old-fashioned blackboard and few slides. Most of the content of the course will be covered by some notes I wrote in these years; for some topics, parts of papers/books will be used. You can download the latest version of these notes from this link.
Lectures
| Date | Lecture | Biblio | |
|---|---|---|---|
| 14/09/2019 | Introduction to the course. Models of computation: RAM, 2-level memory. An example of algorithm analysis: the sum of n numbers, and binary search. The B-tree (or B+-tree) data structure: searching and updating a big-set of sorted keys. Exercise: evaluating the I/O-cost of binary search. | Chap. 1 of the notes. Read note 1 and note 2 on B-trees. | |
| 15/09/2020 | The role of the Virtual Memory system. Algorithm for Permuting. Sorting atomic items: sorting vs permuting, comments on the time and I/O bounds. Finding the maximum-sum subsequence (study from my notes!). | Chapter 2 (no sect 2.5-) | |
| 16/09/2020 | Binary merge-sort, and its I/O-bounds. Snow Plow, with complexity proof and an example. | Chap. 5 of the notes | |
| Students are warmly invited to refresh their know-how about: Divide-and-conquer technique for algorithm design and Master Theorem for solving recurrent relations; and Binary Search Trees | Lecture 2, 9 and 10 of Demaine-Leiserson's course at MIT | ||
| 21/09/2020 | Lecture canceled because of elections | ||
| 22/09/2020 | Multi-way mergesort. Lower bound for sorting: comparisons and I/Os. EXTRA: Lower bound for permuting | Chap. 5 of the notes | |
| 23/09/2020 | Quicksort: recap on best-case, worst-case. Quicksort: Average-case with analysis. Selection of kth ranked item in linear average time (with proof). 3-way partition for better in-memory quicksort. RandSelect. Bounded Quicksort; Multi-way Quicksort: definition, design and I/O-complexity. | ||
| 28/09/2020 | The case of D>1 disks: non-optimality of multi-way MergeSort, the disk-striping technique. The dual pivot. Selection of k-1 “good pivot” via Oversampling. Proof of the average time complexity. | ||
| 29/09/2020 | String sorting: comments on the difficulty of the problem on disk, lower bound. LSD-radix sort with proof of time complexity and correctness. MSD-radix sort and the trie data structure. | Chap. 7 of the notes. | |
| 30/09/2020 | Multi-key Quicksort. Ternary search tree. Exercises. | ||
| Students are warmly invited to refresh their know-how about: hash functions and their properties; hashing with chaining. | Lectures 7 of Demaine-Leiserson's course at MIT | ||
| 05.10.2020 | Hashing and dictionary problem: direct addressing, simple hash functions, hashing with chaining. Uniform hashing and its computing/storage cost, universal hashing (definition and properties). | Chap. 8 of the notes. All theorems with proof, except Theo 8.5 without a proof (only the statement). | |
| 06.10.2020 | Two examples of Universal Hash functions: one with correctness proof, the other without. Perfect hash table (with proof). | ||
| 07.10.2020 | Minimal ordered perfect hashing: definition, properties, construction, space and time complexity. Exercise. | ||
| 12.10.2020 | Cuckoo hashing (with all proofs). | ||
| 13.10.2020 | Bloom Filter: properties, construction, query and insertion operations, error estimation (with proofs). Spectral Bloom Filter. EXTRA: Lower bound on BF space | No 8.7.2 (compressed BF) | |
| 14.10.2020 | Prefix-free codes, the notion of entropy, Shannon Theorem and optimal codes. Integer coding: the problem and some considerations. The codes Gamma and Delta, space/time performance, and consideration on optimal distributions. | Chap. 11 of the notes | |
| 19.10.2020 | The codes Rice, PForDelta, (s,c)-codes, variable-byte. | ||
| 20.10.2020 | Interpolative code. Exercises on integer coders. | ||
| 21.10.2020 | Elias-Fano. With examples. | ||
| 26.10.2020 | Rank and Select: definition and succinct solution for Rank. Compressed solution based on Elias-Fano coding. EXTRA: Solution for Select. | Chapter 15 of the notes | |
| 27.10.2020 | Succinctly encoding binary trees, with examples. Interpolation search. | Sect. 9.2 | |
| 28.10.2020 | Exercises | ||
| This is the end of the topics that will be included in the MidTerm exam of November. | |||
| 02.11.2020 | Lab activity (optional): A gentle introduction to the Succinct Data Structure Library: integer sequences. (Please, prepare in advance the environment for experimenting with the SDSL library, as indicated at the repo.) | See section “Coding Project” above, in collaboration with Giorgio Vinciguerra | |
| 03.11.2020 | Lab activity (optional): More on SDSL about Rank/Select simple and based on Elias-Fano. Coding exercise in class on an array of sorted strings via rank/select data structures. Slides and codes are available here. | See section “Coding Project” above, in collaboration with Giorgio Vinciguerra | |
| 04.11.2020 | Seminar and Lab activity (optional): Learned data structures and their coding. The coding challenge. Slides and codes are available here. | See section “Coding Project” above, in collaboration with Giorgio Vinciguerra | |
| 09.11.2020 | Exercises | ||
| 10.11.2020 | Randomized data structures: Treaps (with proofs). | Notes by others. Study also Theorems and Lemmas. | |
| 11.11.2020 | Midterm exam, fully online | ||
| 16.11.2020 | Randomized data structures: Skip lists (with proofs and comments on I/Os). Random sampling: disk model, known length (algorithms and proofs). Random sampling on the streaming model, known and unknown length. | See Demaine's lecture num. 12 on skip lists, and the notes of the previous lecture. Chap. 3 of the notes. | |
| 17.11.2020 | Reservoir sampling. Algorithm and proofs. | ||
| 18.11.2020 | Fast set intersection, various solutions: scan, sorted merge, binary search, mutual partition, binary search with exponential jumps. Fast set intersection: two-level scan. EXTRA: random shuffling. | Chap. 6 of the notes. | |
| 23.11.2020 | Huffman, with optimality (proof). Canonical Huffman: construction, properties. | Chap. 12 of the notes. No PPM. | |
| 24.11.2020 | Huffman decompression. Arithmetic coding: properties, algorithm and proofs. | ||
| 25.11.2020 | Exercises on Statistical coders | notes | |
| 30.11.2020 | Dictionary-based compressors: properties and algorithmic structure. LZ77, LZSS, LZ78, LZW. | Chap 13, no par 13.4. Slides. | |
| 01.12.2020 | Prefix search: definition of the problem, solution based on arrays, Front-coding, two-level indexing based on compacted tries or Patricia Trees. Analysis of space, I/Os and time of all described solutions. | Chap. 9 of the notes: 9.1, 9.4, 9.5. No Locality Preserving front coding (9.3). | |
| 02.12.2020 | Substring search: definition, properties, reduction to prefix search. The Suffix Array. Binary searching the Suffix Array: p log n. Suffix Array construction via qsort and its asymptotic analysis. LCP array construction in linear time. Text mining use of suffix arrays. | Chap. 10 of the notes: 10.1, 10.2.1 (but no page 10-4 and 10-5 and thus no Lemma 10.2), 10.2.2, 10.2.3 (but no “The skew algorithm”, no “The Scan-based algorithm”), and 10.4.3. | |
| 07.12.2020 | Exercises | notes | |
| 09.12.2020 | Exercises | ||
| 14.12.2020 | Student meeting, before the Final-term exam | ||
| 16.12.2020 | Final term exam, fully online |